How to Recursively Read Elements of a Binary Tree Java Into Array

Binary Tree (with Java Code)
![]()
by Sven Woltmann – May 28, 2021
Two of the most important topics in computer science are sorting and searching data sets. A data construction often used for both is the binary tree and its concrete implementations binary search tree and binary heap. In this article, you will learn: You tin can find the source code for the article in this GitHub repository. A binary tree is a tree information structure in which each node has at well-nigh 2 kid nodes. The child nodes are called left child and right kid. As an example, a binary tree looks like this: Every bit a developer, you should know the following terms: The following image shows the same binary tree data construction as earlier, labeled with node types, node depth, and binary tree height. Earlier we get to the implementation of binary trees and their operations, permit's first briefly await at some special binary tree types. In a full binary tree, all nodes accept either no children or two children. In a complete binary tree, all levels, except perhaps the terminal ane, are completely filled. If the last level is not completely filled, so its nodes are bundled as far to the left every bit possible. A perfect binary tree is a full binary tree in which all leaves have the same depth. A perfect binary tree of height h has northward = twoh+1-ane nodes and l = twoh leaves. At the height of 3, that's xv nodes, 8 of which are leaves. In a counterbalanced binary tree, each node'south left and right subtrees differ in pinnacle by at most one. In a sorted binary tree (also known as ordered binary tree), the left subtree of a node contains just values less than (or equal to) the value of the parent node, and the correct subtree contains only values greater than (or equal to) the value of the parent node. Such a data construction is likewise called a binary search tree. For the binary tree implementation in Java, we first define the data structure for the nodes (class Node in the GitHub repository). For simplicity, we apply The parent reference is not mandatory for storing and displaying the tree. All the same, it is helpful – at least for sure types of binary trees – when deleting nodes. The binary tree itself initially consists only of the interface BinaryTree and its minimal implementation BaseBinaryTree, which initially contains but a reference to the root node: Why nosotros bother to define an interface here will become credible in the further class of the tutorial. The binary tree data structure is thus fully divers. An essential operation on binary trees is the traversal of all nodes, i.e., visiting all nodes in a particular order. The most mutual types of traversal are: In the post-obit sections, you will see the dissimilar types illustrated past the following example: We implement the visiting during traversal using the visitor design design, i.e., nosotros create a visitor object which we laissez passer to the traversal method. In depth-outset search (DFS), we perform the following three operations in a specific order: The standard sequences are: In pre-club traversal (as well known as NLR), traversing is performed in the post-obit social club: The nodes of the example tree are visited in the following lodge, every bit shown in the diagram below: 3→1→13→10→11→16→15→2 The code for this is adequately uncomplicated (DepthFirstTraversalRecursive form, starting at line 21): Y'all can either invoke the method direct – in which example you must pass the the root node to it – or via the non-static method This requires creating an example of An iterative implementation is also possible using a stack (course DepthFirstTraversalIterative from line 20). The iterative implementations are pretty circuitous, which is why I do not impress them hither. You can read why I use In post-club traversal (as well known as LRN), traversing is performed in the following order: In this case, the nodes of the example tree are visited in the following order: xiii→1→11→xv→2→16→x→3 You can observe the code in DepthFirstTraversalRecursive starting at line 42: You can find the iterative implementation, which is fifty-fifty more complicated for mail-order traversal than for pre-order traversal, in DepthFirstTraversalIterative starting at line 44. In-club traversal (also known as LNR) traverses the tree in the post-obit order: The nodes of the example tree are visited in the following guild: 13→one→3→11→10→15→16→2 Y'all will discover the recursive code in DepthFirstTraversalRecursive starting at line 62: See DepthFirstTraversalIterative starting at line 69 for the iterative implementation of in-order traversal. In a binary search tree, in-order traversal visits the nodes in the order in which they are sorted. Reverse in-order traversal (also known as RNL) traverses the tree in the following reverse guild: The nodes of the sample tree are visited in reverse order to the in-order traversal: 2→16→15→10→eleven→iii→1→thirteen Y'all will discover the recursive code in DepthFirstTraversalRecursive starting at line 83: You lot can find the iterative implementation of contrary in-lodge traversal in DepthFirstTraversalIterative starting at line 89. In a binary search tree, reverse in-order traversal visits the nodes in descending sort gild. In breadth-first search (BFS) – also called level-order traversal – nodes are visited starting from the root, level by level, from left to correct. Level-order traversal results in the following sequence: 3→ane→10→thirteen→11→16→15→ii To visit the nodes in level-lodge, nosotros demand a queue in which nosotros commencement insert the root node and then repeatedly remove the get-go element, visit it, and add together its children to the queue – until the queue is empty again. You can find the code in the BreadthFirstTraversal form: You tin observe examples for invoking all traversal types in the Besides traversal, other basic operations on binary copse are the insertion and deletion of nodes. Search operations are provided by special binary trees such as the binary search tree. Without special backdrop, we tin can search a binary tree simply by traversing over all nodes and comparing each with the searched element. When inserting new nodes into a binary tree, we have to distinguish unlike cases: Es ist leicht einen neuen Knoten an ein Blatt oder ein Halbblatt anzuhängen. Hierzu müssen wir lediglich die It is easy to append a new node to a leaf or half leaf. To do this, we just need to set the Merely how do y'all become most inserting a node between an inner node and ane of its children? This is but possible past reorganizing the tree. How exactly the tree is reorganized depends on the concrete blazon of binary tree. In this tutorial, nosotros implement a very simple binary tree and proceed as follows for the reorganization: The following diagram shows the 2d case: Nosotros insert the new node N betwixt P and R: This is – as mentioned – a very simple implementation. In the case higher up, this results in a highly unbalanced binary tree. Specific binary trees take a unlike approach here to maintain a tree structure that satisfies the item properties of the binary tree in question (sorting, balancing, etc.). Here you can encounter the code for inserting a new node with the given (The switch expression with the curly braces was introduced in Java 12/thirteen.) In the Also, when deleting a node, we have to distinguish different cases. If the node Northward to exist deleted is a leaf, i.e., has no children itself, and so the node is simply removed. To do this, we check whether the node is the left or correct child of the parent P and set P's If the node Northward to exist deleted has a kid C itself, and so the kid moves upwards to the deleted position. Once again, we check whether node N is the left or right kid of its parent P. Then, accordingly, nosotros set the How to go along if you want to delete a node with two children? This requires a reorganization of the binary tree. Analogous to insertion, at that place are again unlike strategies for deletion – depending on the concrete type of binary tree. In a heap, for example, the final node of the tree is placed at the position of the deleted node and and so the heap is repaired. We utilise the following easy-to-implement variant for our tutorial: We tin see conspicuously how this strategy leads to a severely unbalanced binary tree. Specific implementations like the binary search tree and the binary heap, therefore, have more circuitous strategies. The following method (class SimpleBinaryTree starting at line 71) removes the passed node from the tree. Corresponding comments mark cases A, B, and C. The In case the deleted node is the root node, we but supplant the In case C (deleting a node with two children), the tree is reorganized as described in the previous section. This is done in the separate method In the Finally, I want to evidence you an culling representation of the binary tree: storing information technology in an array. The array contains every bit many elements as a perfect binary tree of the superlative of the binary tree to be stored, i.e., iih+1-1 elements for height h (in the following image: seven elements for summit 2). The nodes of the tree are sequentially numbered from the root downward, level past level, from left to right, and mapped to the array, equally shown in the following illustration: For a complete binary tree, we can trim the array appropriately – or store the number of nodes as an boosted value. Storing a binary tree every bit an array has the post-obit advantages: Against these, i must weigh the following disadvantages: In this commodity, you lot learned what a binary tree is, what types of binary trees exist, what operations you can utilize to binary trees, and how to implement a binary tree in Java. If you liked the article, feel free to share information technology using one of the share buttons below. Do you lot want to be informed when the next article is published? Then click here to sign upwards for the HappyCoders newsletter.
Binary Tree Definition
Binary Tree Case
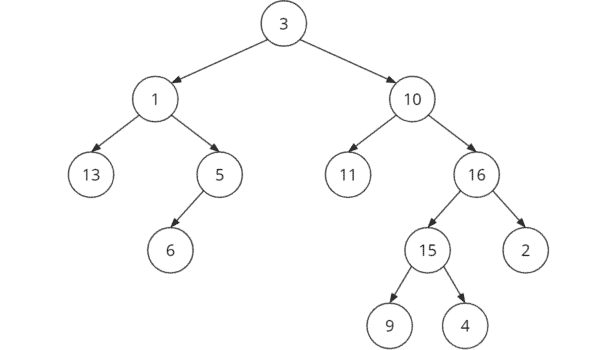
Binary Tree Terminology

Binary Trees Properties
Full Binary Tree

Complete Binary Tree

Perfect Binary Tree

Balanced Binary Tree

Sorted Binary Tree
Binary Tree in Java
int primitives every bit node information. We can, of class, use any other or a generic data type; however, with an int, the code is more than readable – and that is most of import for this tutorial. public course Node { int information; Node left; Node right; Node parent; public Node (int information) { this.data = data; } } public interface BinaryTree { Node getRoot () ; } public class BaseBinaryTree implements BinaryTree { Node root; @Override public Node getRoot () { return root; } } Binary Tree Traversal

Depth-First Search in a Binary Tree
Binary Tree Pre-Order Traversal
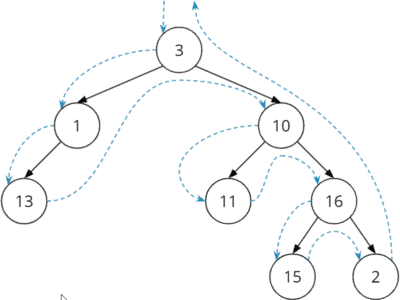
private void traversePreOrder (Node node, NodeVisitor visitor) { if (node == null) { render; } company.visit(node); traversePreOrder(node.left, visitor); traversePreOrder(node.right, company); } traversePreOrder() in the same class (DepthFirstTraversalRecursive, starting at line 17): public void traversePreOrder (NodeVisitor company) { traversePreOrder(tree.getRoot(), visitor); } DepthFirstTraversalRecursive, passing a reference to the binary tree to the constructor: new DepthFirstTraversalRecursive(tree).traversePreOrder(visitor); ArrayDeque instead of Stack in iterative tree traversals hither: Why y'all should not use Stack. Binary Tree Post-Society Traversal

public static void traversePostOrder (Node node, NodeVisitor company) { if (node == nada) { render; } traversePostOrder(node.left, visitor); traversePostOrder(node.correct, company); visitor.visit(node); } Binary Tree In-Order Traversal

public static void traverseInOrder (Node node, NodeVisitor company) { if (node == null) { return; } traverseInOrder(node.left, company); visitor.visit(node); traverseInOrder(node.right, visitor); } Binary Tree Reverse In-Guild Traversal

public static void traverseReverseInOrder (Node node, NodeVisitor visitor) { if (node == null) { return; } traverseReverseInOrder(node.right, visitor); visitor.visit(node); traverseReverseInOrder(node.left, visitor); } Binary Tree Level-Order Traversal

public static void traverseLevelOrder (Node root, NodeVisitor visitor) { if (root == nada) { return; } Queue<Node> queue = new ArrayDeque<>(); queue.add together(root); while (!queue.isEmpty()) { Node node = queue.poll(); visitor.visit(node); if (node.left != cypher) { queue.add(node.left); } if (node.right != null) { queue.add(node.right); } } } traverseTreeInVariousWays() method of the Example1 form. Binary Tree Operations
Insertion of a Node
Case A: Inserting a Node Below a (One-half) Leaf
left- oder right-Referenz des Parent-Knotens P, an den wir den neuen Knoten N anhängen wollen, auf den neuen Knoten setzen. Wenn wir auch mit parent-Referenzen arbeiten, müssen wir diese im neuen Knoten N auf den Parent-Knoten P setzen.left or right reference of the parent node P, to which nosotros want to append the new node N, to the new node. If we are working with a parent reference, we demand to fix the new node's parent reference to P.

Case B: Inserting a Node Betwixt Inner Node and Its Child


Inserting a Binary Tree Node – Java Source Code
data below the given parent node to the specified side (left or correct) using the reorganization strategy defined in the previous section (class SimpleBinaryTree starting at line 18). public Node insertNode (int data, Node parent, Side side) { var node = new Node(data); node.parent = parent; switch (side) { instance LEFT -> { if (parent.left != cipher) { node.left = parent.left; node.left.parent = node; } parent.left = node; } case Correct -> { if (parent.right != zip) { node.right = parent.correct; node.right.parent = node; } parent.right = node; } default -> throw new IllegalStateException(); } return node; } createSampleTree() method of the Example1 class, you tin meet how to create the sample binary tree from the beginning of this article. Deletion of a Node
Case A: Deleting a Node Without Children (Foliage)
left or correct reference to null appropriately.
Case B: Deleting a Node With I Child (Half Leafage)
left or right reference of P to N's child C (the previous grandchild) – and C'due south parent reference to Northward's parent P (the previous grandparent node).
Instance C: Deleting a Node With Ii Children


Deleting a Tree Node – Java Source Code
public void deleteNode (Node node) { if (node.parent == zilch && node != root) { throw new IllegalStateException("Node has no parent and is not root"); } // Case A: Node has no children --> set node to nada in parent if (node.left == null && node.right == nada) { setParentsChild(node, aught); } // Example B: Node has ane child --> replace node by node's child in parent // Case B1: Node has only left kid else if (node.right == null) { setParentsChild(node, node.left); } // Example B2: Node has only correct kid else if (node.left == cipher) { setParentsChild(node, node.right); } // Case C: Node has two children else { removeNodeWithTwoChildren(node); } // Remove all references from the deleted node node.parent = naught; node.left = null; node.right = goose egg; } setParentsChild() method checks whether the node to be deleted is the left or right child of its parent node and replaces the corresponding reference in the parent node with the child node. kid is null if the node to exist deleted has no children, and accordingly, the kid reference in the parent node is set to null.root reference. private void setParentsChild (Node node, Node child) { // Node is root? Has no parent, set root reference instead if (node == root) { root = kid; if (kid != cipher) { child.parent = naught; } render; } // Am I the left or correct child of my parent? if (node.parent.left == node) { node.parent.left = child; } else if (node.parent.right == node) { node.parent.correct = child; } else { throw new IllegalStateException( "Node " + node.data + " is neither a left nor a right child of its parent " + node.parent.data); } if (child != goose egg) { child.parent = node.parent; } } removeNodeWithTwoChildren(): private void removeNodeWithTwoChildren (Node node) { Node leftTree = node.left; Node rightTree = node.right; setParentsChild(node, leftTree); // find correct-most child of left tree Node rightMostChildOfLeftTree = leftTree; while (rightMostChildOfLeftTree.right != null) { rightMostChildOfLeftTree = rightMostChildOfLeftTree.right; } // append correct tree to right kid rightMostChildOfLeftTree.correct = rightTree; rightTree.parent = rightMostChildOfLeftTree; } deleteSomeNodes() method of the Example1 class, you can see how some nodes of the example tree are deleted again. Array Representation of a Binary Tree

Advantages and Disadvantages of the Array Representation
For a node at index i,
Summary
constantinothinscion1974.blogspot.com
Source: https://www.happycoders.eu/algorithms/binary-tree-java/
0 Response to "How to Recursively Read Elements of a Binary Tree Java Into Array"
Post a Comment